En nuestra jornada por comprender las formas geométricas básicas, el círculo emerge como una figura simple pero fundamental. En este artículo, nos adentraremos en los intrincados detalles del círculo, desde sus partes constituyentes hasta las fórmulas matemáticas que lo gobiernan. Acompáñanos mientras exploramos este fascinante mundo de curvas y proporciones.
Indique a continuación cualquier valor para calcular los valores restantes de un círculo.
Calculadora de Círculo
Seleccione qué valor desea ingresar:
Ingrese el valor:
Seleccione la unidad de medida:
Resultados:
Radio:
Diámetro:
Circunferencia:
Área:
Definición y Partes del Círculo
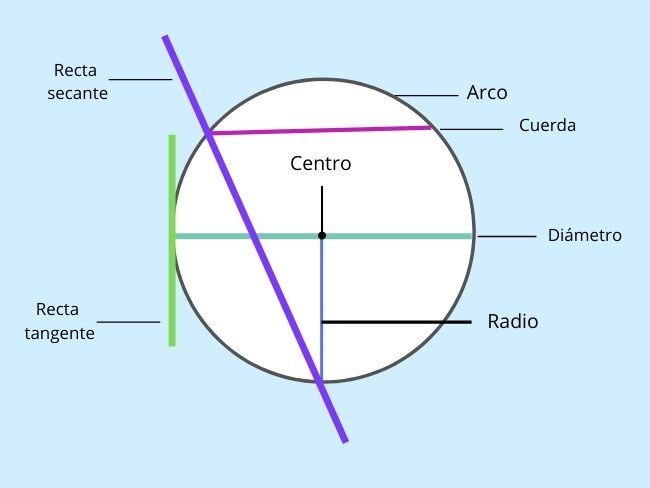
Un círculo, geométricamente hablando, es una figura cerrada simple. Más específicamente, es un conjunto de todos los puntos en un plano que están equidistantes de un punto dado, llamado el centro. Esta definición establece la base para comprender sus componentes principales:
Centro (o origen):
Es el punto dentro del círculo que está equidistante de todos los demás puntos en el círculo.
Radio:
Es la distancia entre cualquier punto en el círculo y el centro del mismo. Es igual a la mitad de la longitud del diámetro.
Diámetro:
Es la distancia más larga entre dos puntos en un círculo; por definición, el diámetro del círculo siempre pasará a través del centro del mismo. Es igual al doble de la longitud del radio.
Circunferencia:
Es la distancia alrededor del círculo, o la longitud de un circuito a lo largo del círculo.
Arco:
Parte de la circunferencia de un círculo. Puede ser un arco mayor (más grande que la mitad de la circunferencia) o un arco menor (menor que la mitad de la circunferencia).
Cuerda:
Es un segmento de línea que va de un punto a otro en el círculo. Una cuerda que pasa por el centro del círculo es un diámetro del mismo.
Secante:
Es una línea que atraviesa el círculo en dos puntos; es una extensión de una cuerda que comienza y termina fuera del círculo.
Tangente:
Es una línea que intersecta el círculo en un solo punto; el resto de la línea, excepto el punto único en el que intersecta el círculo, se encuentra fuera del mismo.
Sector:
Es el área de un círculo creada entre dos radios. Puede ser un sector mayor (con un ángulo central mayor que 180°) o un sector menor (con un ángulo central menor que 180°).
El Constante π y Fórmulas del Círculo
El radio, el diámetro y la circunferencia de un círculo están todos relacionados a través de la constante matemática π, o pi, que es la razón entre la circunferencia de un círculo y su diámetro. El valor de π es aproximadamente 3.14159, un número irracional que nunca termina ni tiene un patrón repetitivo permanente en su representación decimal.
En el pasado, los antiguos geómetras dedicaron mucho tiempo en un esfuerzo por «cuadrar el círculo», un proceso que implicaba intentar construir un cuadrado con la misma área que un círculo dado en un número finito de pasos utilizando solo un compás y una regla. Aunque ahora sabemos que esto es imposible, no fue hasta 1880 que Ferdinand von Lindemann presentó una prueba de que π es trascendental, lo que puso fin a todos los esfuerzos por «cuadrar el círculo». Aunque los esfuerzos de los antiguos geómetras puedan parecer cómicos o inútiles hoy en día, es gracias a personas como estas que tantos conceptos matemáticos están bien definidos en la actualidad.
Fórmulas del círculo
Las fórmulas básicas del círculo son:
- D=2R
- C=2πR
- A=πR2
Donde:
- R: Radio
- D: Diámetro
- C: Circunferencia
- A: Área
- π: 3.14159
¡Ahora estás armado con un conocimiento completo sobre el círculo y sus propiedades! Ya sea que estés resolviendo problemas geométricos o simplemente admirando la belleza de esta forma, esperamos que este artículo te haya proporcionado una comprensión más profunda y una apreciación renovada por una de las figuras más simples pero más importantes en la geometría.